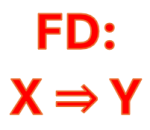Functional Dependency (FD) là lý thuyết quan trọng trong Relational Database (RD), làm tiền đề cho các Normal Forms: 2NF, 3NF, và BCNF.
Định nghĩa
FD là một khái niệm quan trọng trong lý thuyết RD, được sử dụng để xác định mối quan hệ giữa các thuộc tính (attributes) trong một bảng dữ liệu (relation):
Giá trị của một thuộc tính (hoặc một tập hợp thuộc tính) có thể xác định duy nhất giá trị của một thuộc tính khác.
Ký hiệu:
FD giữa hai tập hợp thuộc tính X và Y trong một relation: X ⇒ Y:
-
Giá trị của X xác định duy nhất giá trị của Y.
-
X được gọi là tập xác định (determinant), Y được gọi là tập phụ thuộc (dependent)
FD tầm thường - trivial FD
Một FD X ⇒ Y được gọi là tầm thường nếu Y ⊂ X. (Y là tập con của X). Y là tập con của X khi và chỉ khi mọi phần tử trong Y đều thuộc X.
Ví dụ: X = {A, B, C, D}, Y = {C, D}
Giả sử ta có relation sau:
| roll_no | name | age |
| 42 | abc | 17 |
| 43 | pqr | 18 |
| 44 | xyz | 18 |
Ta có các FD tầm thường sau:
{roll_no, name} ⇒ {name}
{roll_no, name} ⇒ {roll_no}
{roll_no, age} ⇒ {age}
{roll_no} ⇒ {roll_no}
FD không tầm thường - nontrivial FD
Một FD X ⇒ Y được gọi là không tầm thường nếu Y ⊄ X.
Với relation bên trên, ta có các FD không tầm thường sau:
{roll_no} ⇒ {name}
{roll_no} ⇒ {age}
{roll_no, name} ⇒ {age}
Phụ thuộc một phần - Partial Dependency (PD)
Một FD X⇒Y trở thành một PD khi Y được xác định bởi X và Y cũng được xác định bởi một tập con của X, với X là một Candidate Key.
Tham khảo Candidate key ở đây.
Ví dụ, có relation:
| OrderID | ProductID | ProductName | Quantity | ProductPrice |
| 1 | 101 | Laptop | 2 | 1000 |
| 1 | 102 | Mouse | 5 | 20 |
| 2 | 101 | Laptop | 1 | 1000 |
| 2 | 103 | Keyboard | 3 | 50 |
| 3 | 101 | Laptop | 1 | 1000 |
Candidate key: {OrderID, ProductID}.
Ta có các PD sau:
{ProductID} ⇒ {ProductName}
{ProductID} ⇒ {ProductPrice}
{ProductID} ⇒ {ProductName, ProductPrice}
do ProductID là subkey của candidate key {OrderID, ProductID}.
Một số tính chất
Tính phản xạ - reflexive
A ⇒ A: Nếu biết A, có thể suy ra A.
Ngoài ra, ta còn biết: AA ⇒ A và A ⇒ AA
Tính gia tăng - augmentation
Nếu A ⇒ B thì AC ⇒ B.
Nghĩa là nếu thêm thông tin vào LHS (left hand side) thì ta vẫn có thể suy ra RHS (right hand side).
Tính phân rã - decomposition
Nếu A ⇒ BCD thì ta có A ⇒ B, A ⇒ C, và A ⇒ D.
Tính hợp - union
Nếu A ⇒ B và A ⇒ C thì A ⇒ BC.
Tính bắc cầu - transitive
Nếu A ⇒ B và B ⇒ C thì A ⇒ C.
Tập con - subset
Nếu A là một tập con của tập cha F thì F ⇒ A.
Bài tập
Bài 1: Cho R(ABCD) với các FD:
A ⇒ B
B ⇒ C
AB ⇒ D
Tìm các PD nếu có.
Bài 2: Cho R(ABC) với các FD:
AB ⇒ C
C ⇒ A
Tìm các PD nếu có.
Bài 3: Cho R(ABCD) với các FD:
A ⇒ B
AB ⇒ C
BC ⇒ D
Tìm các PD nếu có.
Bài 4: Cho R(ABCD) với các FD:
A ⇒ B
B ⇒ C
C ⇒ D
AD => B
Tìm các PD nếu có.
Đáp án
Với các bài toán tìm Partial Dependency (PD), cách làm của ta là phải tìm Candidate key do PD được định nghĩa với vế trái là subkey của Candidate key đó. Sau đó, ta đối chiếu từng FD xem có FD nào có vế trái là Subkey không.
Bài 1:
Từ A ⇒ B và B ⇒ C ta có A ⇒ BC (áp dụng tính bắc cầu và tính hợp).
Từ A ⇒ BC ta cũng có AA ⇒ ABC (tính phản xạ), và ta còn có AB ⇒ D nên sử dụng tính bắc cầu ta có A+ => BCD.
Vậy A là Candidate Key.
Từ B ⇒ C ta có AB => AC và tiếp theo ta có AB => ABC (tính gia tăng và phản xạ).
Do AB ⇒ D nên sử dụng tính hợp, ta có: AB ⇒ ABCD hay AB+ ⇒ CD.
Nhưng AB không phải là Candidate key do ta có A là Candidate key rồi.
Tóm lại, A là Candidate key của relation trên.
Đối chiếu từng FD trong đề bài, ta thấy không có FD nào có vế trái là subkey của A. Vậy relation không tồn tại FD.
Bài 2: Cho R(ABC) với các FD:
AB ⇒ C
C ⇒ A
Tìm các PD nếu có.
Tương tự, ta xét
AB ⇒ C nên dĩ nhiên AB+ ⇒ C tức AB là Candidate key.
Từ C ⇒ A ta có CB ⇒ AB hay BC+ ⇒ ABC. Vậy ta có tiếp một Candidate key nữa là BC.
Đối chiếu hai FD ban đầu với hai Candidate key vừa tìm được, ta có các PD sau:
C ⇒ A
Các bài tiếp theo tương tự.
Tham khảo: